# Estimate the variance for Gene A
var(recentered_expression_matrix[, "Gene_A"])[1] 799.3333Will Gammerdinger, Noor Sohaili
September 5, 2025
There are a couple properties of variance and co-variance that we can verify:
cov(X,X) is equal to var(X). We can observe this is mathematically below:
As a result, you will sometimes see covariance matrices written as:
# Estimate the covariance for Gene A and Gene A
cov(recentered_expression_matrix[, "Gene_A"], recentered_expression_matrix[, "Gene_A"])[1] 799.3333# Extract the covariance estimate of Gene A and Gene A from the covariance matrix
cov_matrix["Gene_A", "Gene_A"][1] 799.3333Estimate the covariance of Gene B and Gene A.
# Estimate the covariance of Gene B and Gene A
cov(recentered_expression_tibble[, "Gene_B"], recentered_expression_tibble[, "Gene_A"]) Gene_A
Gene_B 584.6667It is the same.
When looking at the percent explained by each principal component, the first principal component should explain the most and each of the following principal components should explain less than the previous principal component. Let’s have a look at our pct_var_explained object, are our results congruent with this expectation?
Yes, PC_1 explains 96.1672305 and PC_2 explains 3.8327695
Create a plot of the Principal Components Analysis derived from prcomp(). Is it the same as the plot we derived except only rotated 180°?
# Create a tibble to hold the PC scores prcomp() found and also make the Cell IDs into a column
prcomp_pc_scores_tibble <- prcomp_PCA$x %>%
as.data.frame() %>%
rownames_to_column("cells") %>%
as_tibble()
# Plot the PC scores found by prcomp()
ggplot(prcomp_pc_scores_tibble, aes(x = PC1, y = PC2, label = cells)) +
geom_point( color = "cornflowerblue") +
geom_text(hjust = 0, vjust = -1) +
theme_bw() +
xlim(-50, 50) +
ylim(-12, 12) +
xlab(paste0("PC 1 (Variance Explained ", round(prcomp_eigenvalues["PC_1"]/sum(prcomp_eigenvalues) * 100, digits = 2),"%)")) +
ylab(paste0("PC 2 (Variance Explained ", round(prcomp_eigenvalues["PC_2"]/sum(prcomp_eigenvalues) * 100, digits = 2),"%)")) +
ggtitle("PCA of Expression Values from Four Cells") +
theme(plot.title = element_text(hjust = 0.5))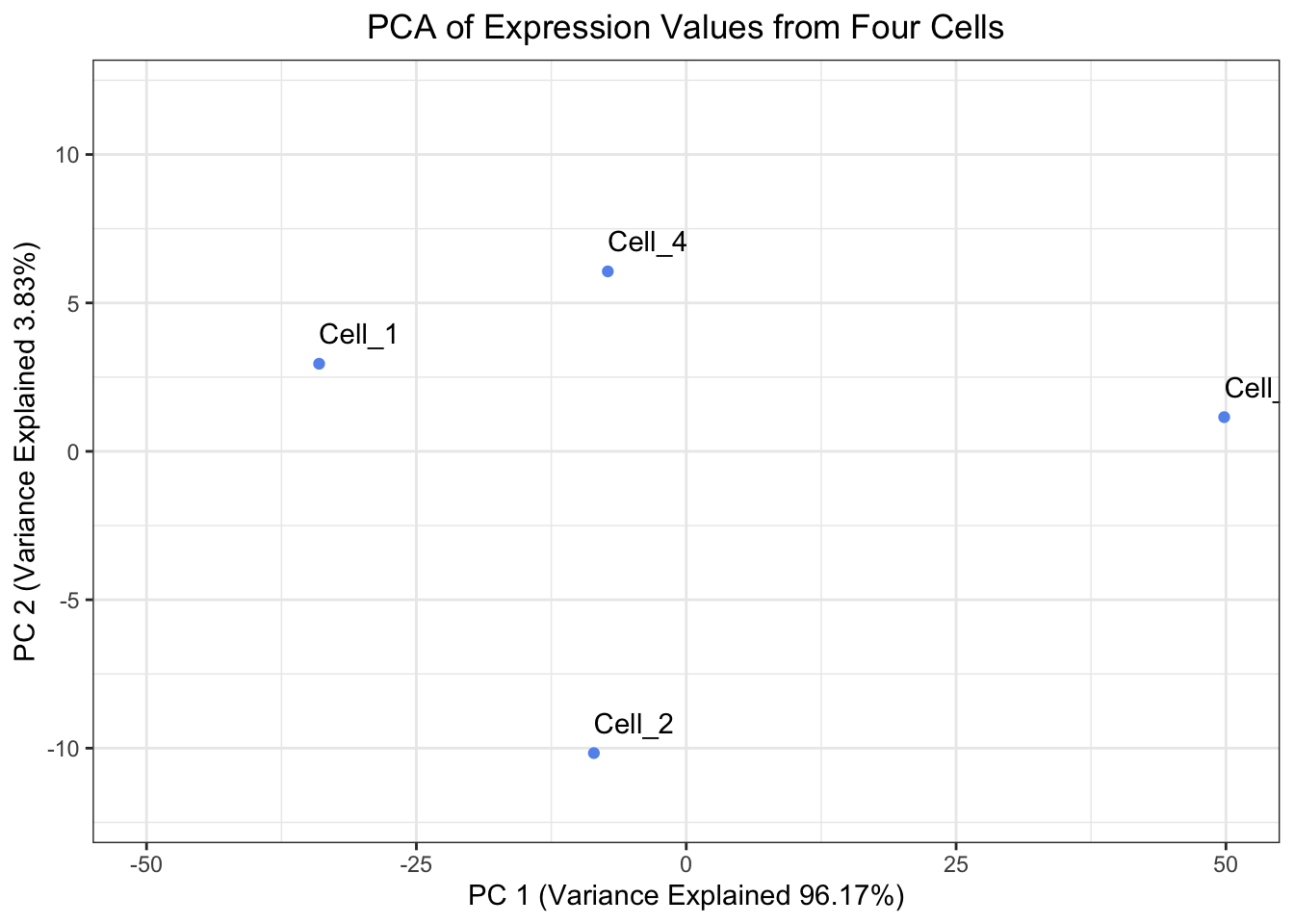
Yes, it is the same plot just rotated 180°.
---
title: "Theory of PCA - Answer Key"
authors: "Will Gammerdinger, Noor Sohaili"
date: "Friday, September 5, 2025"
editor_options:
markdown:
wrap: 72
---
```{r}
#| label: load_data
#| echo: false
# Items to pre-load
library(tidyverse)
# Create a vector for Cell IDs
cells <- c("Cell_1", "Cell_2", "Cell_3", "Cell_4")
# Create a vector to hold expression values for Gene A across all of the cells
Gene_A <- c(0, 12, 65, 23)
# Create a vector to hold expression values for Gene B across all of the cells
Gene_B <- c(4, 30, 57, 18)
# Create a tibble to hold the cell names and expression values
expression_tibble <- tibble(cells, Gene_A, Gene_B)
# Determine the center of the data by:
# Finding the average expression of gene A
Gene_A_mean <- mean(expression_tibble$Gene_A)
# Finding the average expression of gene B
Gene_B_mean <- mean(expression_tibble$Gene_B)
# Create a vector to hold the center of the data
center_of_data <- c(Gene_A_mean, Gene_B_mean)
# Assign names to the components of the vector
names(center_of_data) <- c("Gene_A", "Gene_B")
# Shift the data points so that they data is centered on the origin
recentered_expression_tibble <- expression_tibble %>%
mutate(
Gene_A = Gene_A - Gene_A_mean,
Gene_B = Gene_B - Gene_B_mean
)
# Move the cell IDs to the rownames and convert the tibble to a matrix
recentered_expression_matrix <- recentered_expression_tibble %>%
column_to_rownames("cells") %>%
as.matrix()
# Create a covariance matrix
cov_matrix <- cov(recentered_expression_matrix)
# Find the eigenvalues and eigenvectors of the covariance matrix
eig <- eigen(cov_matrix)
# Transform the data into PC space by multiply the re-centered expression matrix by the eigenvectors
pc_scores <- recentered_expression_matrix %*% eig$vectors
# Name the columns in pc_scores object
colnames(pc_scores) <- c("PC_1", "PC_2")
# Calculate the percent of variance explained by each PC using the eigenvalues
pct_var_explained <- (eig$values / sum(eig$values)) * 100
# Name the elements of the pct_var_explained by their PC
names(pct_var_explained) <- c("PC_1", "PC_2")
# Create a tibble to hold the PC scores we found and also make the Cell IDs into a column
pc_scores_tibble <- pc_scores %>%
as.data.frame() %>%
rownames_to_column("cells") %>%
as_tibble()
# Run prcomp() on the expression tibble after moving the Cell IDs to be rownames
prcomp_PCA <- expression_tibble %>%
column_to_rownames("cells") %>%
prcomp()
# Print the eigenvalues found by prcomp() by squaring prcomp_PCA$sdev
prcomp_eigenvalues <- prcomp_PCA$sdev ** 2
# Name the elements of the prcomp_eigenvalues by their PC
names(prcomp_eigenvalues) <- c("PC_1", "PC_2")
```
# Exercise 1
There are a couple properties of variance and co-variance that we can verify:
*cov(X,X)* is equal to *var(X)*. We can observe this is mathematically below:
<img src="https://latex.codecogs.com/svg.image?&space;cov(X,X)=\frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\bar{x})(x_{i}-\bar{x})=\frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}=var(X)" width="500">
As a result, you will sometimes see covariance matrices written as:
<img src="https://latex.codecogs.com/svg.image?\begin{bmatrix}var(X)&cov(X,Y)&...&cov(X,Z)\\cov(Y,X)&var(Y)&...&cov(Y,Z)\\...&...&...&...\\cov(Z,X)&cov(Z,Y)&...&var(Z)\\\end{bmatrix}" width="300">
1. Confirm this property by estimating the variance for Gene A.
```{r covariance_check_1}
# Estimate the variance for Gene A
var(recentered_expression_matrix[, "Gene_A"])
```
2. Now estimate the covariance for Gene A and Gene A
```{r covariance_check_2}
# Estimate the covariance for Gene A and Gene A
cov(recentered_expression_matrix[, "Gene_A"], recentered_expression_matrix[, "Gene_A"])
```
3. Is the value the same? Does it match the value in the covariance matrix for Gene A and Gene A?
```{r covariance_matrix_check}
# Extract the covariance estimate of Gene A and Gene A from the covariance matrix
cov_matrix["Gene_A", "Gene_A"]
```
4. *cov(X,Y)* is equal to *cov(Y,X)*. We can observe this is mathematically below:
<img src="https://latex.codecogs.com/svg.image?&space;cov(X,Y)=\frac{1}{n-1}\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})=\frac{1}{n-1}\sum_{i=1}^{n}(y_{i}-\bar{y})(x_{i}-\bar{x})=cov(Y,X)" width="500">
Estimate the covariance of Gene B and Gene A.
```{r covariance_check_3}
# Estimate the covariance of Gene B and Gene A
cov(recentered_expression_tibble[, "Gene_B"], recentered_expression_tibble[, "Gene_A"])
```
5. How does this compare to the covariance that we estimated by hand?
It is the same.
# Exercise 2
When looking at the percent explained by each principal component, the first principal component should explain the most and each of the following principal components should explain less than the previous principal component. Let's have a look at our `pct_var_explained` object, are our results congruent with this expectation?
```{r pct_explained}
pct_var_explained
```
Yes, `PC_1` explains `r pct_var_explained[1]` and `PC_2` explains `r pct_var_explained[2]`
# Exercise 3
Create a plot of the Principal Components Analysis derived from `prcomp()`. Is it the same as the plot we derived except only rotated 180°?
```{r plotting_PCA_prcomp}
# Create a tibble to hold the PC scores prcomp() found and also make the Cell IDs into a column
prcomp_pc_scores_tibble <- prcomp_PCA$x %>%
as.data.frame() %>%
rownames_to_column("cells") %>%
as_tibble()
# Plot the PC scores found by prcomp()
ggplot(prcomp_pc_scores_tibble, aes(x = PC1, y = PC2, label = cells)) +
geom_point( color = "cornflowerblue") +
geom_text(hjust = 0, vjust = -1) +
theme_bw() +
xlim(-50, 50) +
ylim(-12, 12) +
xlab(paste0("PC 1 (Variance Explained ", round(prcomp_eigenvalues["PC_1"]/sum(prcomp_eigenvalues) * 100, digits = 2),"%)")) +
ylab(paste0("PC 2 (Variance Explained ", round(prcomp_eigenvalues["PC_2"]/sum(prcomp_eigenvalues) * 100, digits = 2),"%)")) +
ggtitle("PCA of Expression Values from Four Cells") +
theme(plot.title = element_text(hjust = 0.5))
```
Yes, it is the same plot just rotated 180°.